Obesity phase 2 - Exploring usage of FAT with a negative connotation

Exploring usage of the lemma FAT

There is interest in exploring statistics around the use of the word “fat” with a negative connotation around the following research questions:

Do tabloids use “fat” with a negative connotation more than broadsheets?
Or do broadsheets use “fat” with a negative connotation more than tabloids?
Or is there no discernible pattern of use?
Is there any newspaper that uses fat with a negative connotation more than others?
Any year where fat with a negative connotation is the most frequent/least frequent?

Additional question:

Is there a difference of use by primary topic?

Executive summary

1. Tabloids use the word “fat” in a negative context more frequently than broadsheets.

More specifically, a Welch Two Sample t-test testing the difference between the frequency in broadsheets per 1000 words and frequency in tabloids (mean of broadsheets = 2.62, mean of tabloids = 4.49) suggests that the effect is negative, statistically significant, and small (difference = -1.87, 95% CI [-2.18, -1.56], t(2251.24) = -11.73, p < .001; Cohen’s d = -0.47, 95% CI [-0.55, -0.39])
The total number of uses of “fat” we observe is higher in tabloids and lower in broadsheets than we would expect based on the word count in these subcorpora (p < 0.001).
The number of articles with use of “fat” we observe is not different between tabloids and broadsheets.

2. Tabloids have shorter article lengths than broadsheets, as demonstrated in the analysis of obese.

3. In this case (but not that of obese or overweight), bootstrap re-sampling of the counts of use of the word “fat” in a negative connotation revealed that raw counts were higher in broadsheets than in tabloids (so the opposite of the above result), in part due to more articles in broadsheets having 7+ uses vs only tabloids (23 vs 10 articles, respectively). So the result described above is in part attributable to the longer length of articles in broadsheets vs tabloids.

4. Investigating the data by source and year revealed that these variables explained a small amount of variance in the data, with the word fat being used less frequently in the Age, Australian, Canberra Times and Sydney Morning Herald had a lower frequency of use of the word “fat” relative to the Advertiser, while in the Northern Territorian the word “fat” was used somewhat more frequently than in the Advertiser. The word “fat” was not used differently in the corpus across the time period.

4. Significant differences in the use of “fat” were observed in articles on different topics, with articles annotated as “Awards”, “Women and Pregnancy” and “Bio-medical Research” using more instances per 1000 words than articles discussing “Students and teachers”, “Politics” and “Food”.

5. Significant differences in article topics were also observed between tabloids and broadsheets, as discussed in the analysis of obese.

Data source

CQPweb data was provided. To calculate normalised frequency, we divide the number of observations from CQPweb by the word count as calculated in Python, and multiple by 1000.

Code

library(here)
library(janitor)
library(readr)
library(dplyr)
library(ggplot2)
library(tidyr)
library(knitr)
library(report)
theme_set(theme_minimal())
library(patchwork)
library(ggfortify)
source(here::here("400_analysis", "functions.R"))

Code

adj_fat <- read_csv(here("200_data_clean", "fat_annotated.csv"))
topic_labels <- read_csv(here("100_data_raw", "topic_labels.csv"))
fat_annotated <- inner_join(
  adj_fat, topic_labels, by = c("dominant_topic" = "topic_number")) %>% 
  mutate(frequency = 10^3*no_hits_in_text/wordcount_total) 
metadata <- read_csv(here("100_data_raw", "corpus_cqpweb_metadata.csv"))
additional_source_metadata <- read_csv(here("100_data_raw", "addition_source_metadata.csv"))
topic_labels <- read_csv(here("100_data_raw", "topic_labels.csv"))
metadata_full <- inner_join(inner_join(metadata,
                                       topic_labels,
                                       by = c("dominant_topic" = "topic_number")),
                            additional_source_metadata)

We group articles into tabloids and broadsheets, and by orientation, in the following manner:

Code

metadata_full |>
  select(source, source_type, orientation) |>
  distinct() |>
  kable()

Table 1: Classification of sources into types and by orientation.
source	source_type	orientation
Advertiser	tabloid	right
Australian	broadsheet	right
NorthernT	tabloid	right
CourierMail	tabloid	right
Age	broadsheet	left
SydHerald	broadsheet	left
Telegraph	tabloid	right
WestAus	tabloid	right
CanTimes	broadsheet	left
HeraldSun	tabloid	right
HobMercury	tabloid	right
BrisTimes	broadsheet	left

Tabloid vs broadsheet

What is the distribution of “fat” used with a negative connotation in articles?

Code

fat_annotated %>%
  ggplot(aes(x = no_hits_in_text, fill = source_type)) +
  geom_bar(position = "dodge2") +
  labs(
    x = "Number of hits in article, CQPWeb",
    y = "Number of articles in corpus",
    fill = "Source type"
  )
no_articles_broadsheet <- metadata_full %>% 
  filter(source_type == "broadsheet") %>% nrow()
no_articles_tabloid <- metadata_full %>% 
  filter(source_type == "tabloid") %>% nrow()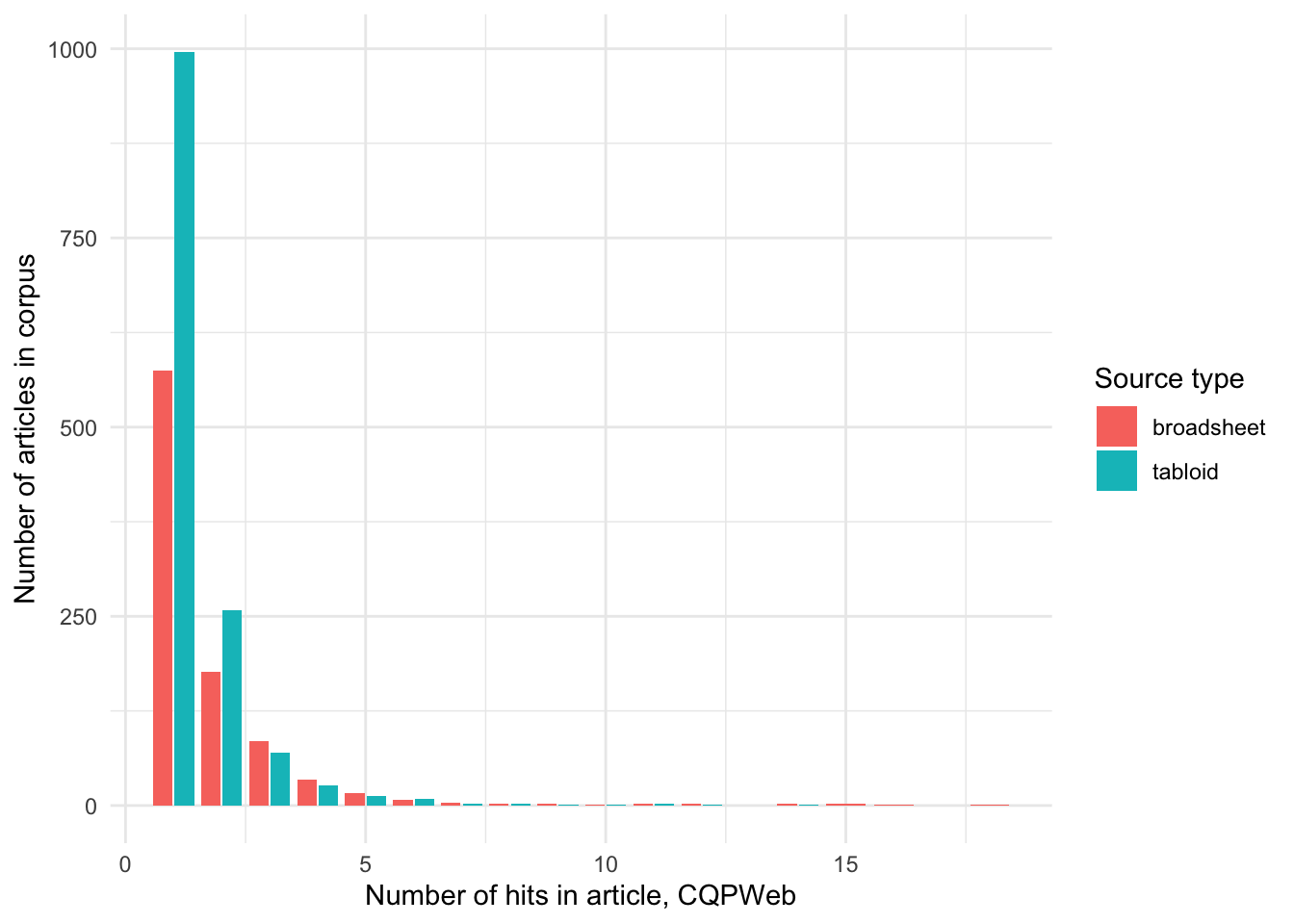

Figure 1: Number of uses of FAT across articles from broadsheets and tabloids.

It seems like there is more usage in tabloids than broadsheets. Let’s divide the numbers by the total number of articles in tabloids/broadsheets, respectively.

Code

fat_annotated %>%
  group_by(source_type, no_hits_in_text) %>%
  count() %>%
  pivot_wider(names_from = source_type, values_from = n, values_fill = 0) %>%
  mutate(broadsheet = 1000*broadsheet/no_articles_broadsheet,
         tabloid = 1000*tabloid/no_articles_tabloid) %>%
  pivot_longer(cols = c(broadsheet, tabloid)) %>%
  ggplot(aes(x = no_hits_in_text, y=value, fill = name)) +
  geom_bar(position = "dodge2", stat="identity") +
  labs(
    x = "Number of hits in article, CQPWeb",
    y = "Normalised number of articles, per 1000, in corpus",
    fill = "Source type"
  )

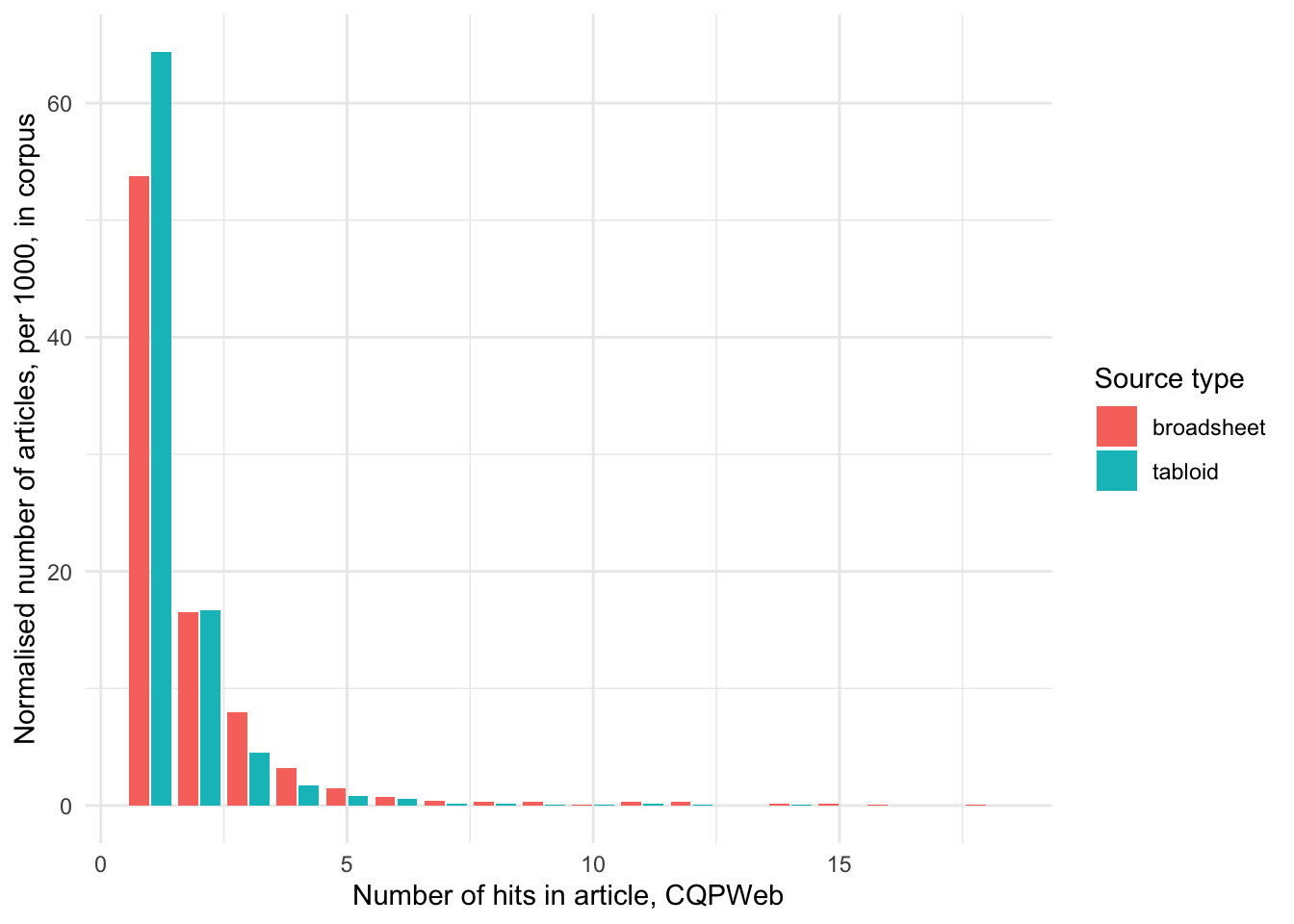
Figure 2: Number of uses of FAT across articles from broadsheets and tabloids, normalised to the number of articles in tabloids and broadsheets in which FAT is used.

We can see that the trend of higher usage holds true for tabloids even if we consider that tabloids contribute more articles to the corpus than broadsheets.

How is this usage distributed by year (number of articles in corpus)?

Code

fat_annotated_filtered <- fat_annotated %>%
  # these sources are already not present in the data, but we will
  # retain this code chunk as it keeps consistency of variable names with
  # other files in work, including for obese and overweight
  filter(!(source %in% c("BrisTimes", "Telegraph")))
assess_year_source(fat_annotated)

Table 2: Number of articles that use FAT by year and source.
source	2008	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018	2019	Total
Advertiser	34	39	27	28	29	39	25	28	17	18	11	9	304
Age	53	24	17	16	24	22	23	24	18	15	13	3	252
Australian	27	21	18	19	11	10	19	6	10	13	9	9	172
CanTimes	19	12	11	19	13	15	20	14	10	10	12	1	156
CourierMail	48	43	26	30	27	32	29	27	24	22	17	14	339
HeraldSun	65	54	50	50	36	35	26	18	24	18	9	6	391
HobMercury	19	14	12	12	9	11	5	3	6	9	8	4	112
NorthernT	19	14	9	4	6	7	10	0	5	7	2	2	85
SydHerald	41	43	38	27	31	29	27	27	25	22	18	10	338
WestAus	26	24	17	20	14	13	15	5	11	3	1	2	151
Total	351	288	225	225	200	213	199	152	150	137	100	60	2300

How is the frequency (per thousand words) of the usage of fat distributed by tabloids/broadsheets?

Code

fat_annotated_filtered %>%
  ggplot(aes(x = source_type, y = log(frequency))) + 
  geom_boxplot() + 
  labs(
    x = "Source type",
    y = "log(frequency per 1000 words)"
  )

Figure 3: Frequency per 1000 words of usage of FAT in tabloids and broadsheets.

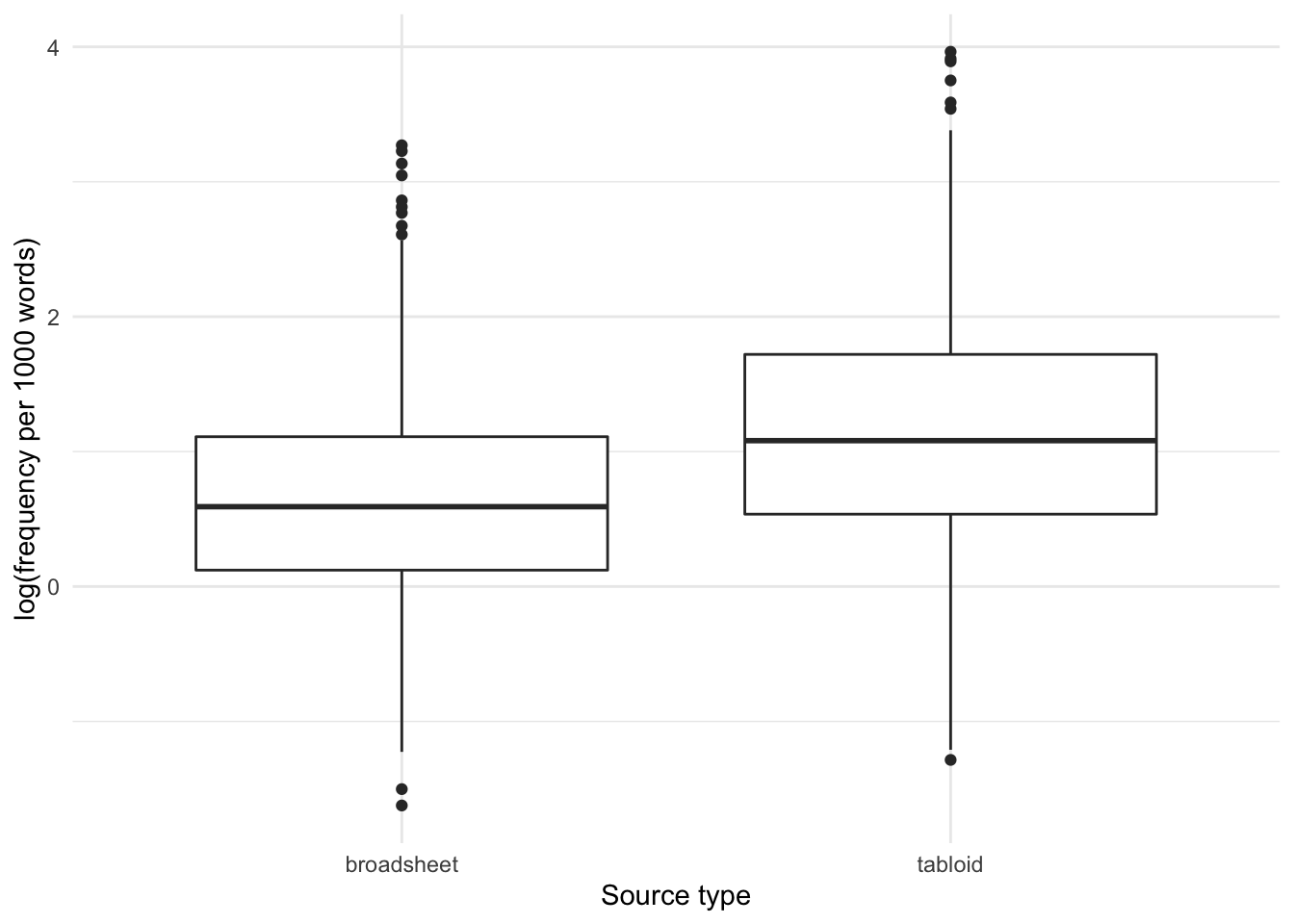
We can see that the frequency is slightly higher in tabloids than in broadsheets.

And let’s also use a histogram to look at the distribution:

Code

fat_annotated_filtered %>%
  ggplot(aes(fill = source_type,x = log(frequency))) + 
  geom_histogram() + 
  labs(
    fill = "Source type",
    x = "log(frequency per 1000 words)",
    y = "Number of articles"
  )

Figure 4: Histogram of the distribution of usage of FAT in tabloids and broadsheets.

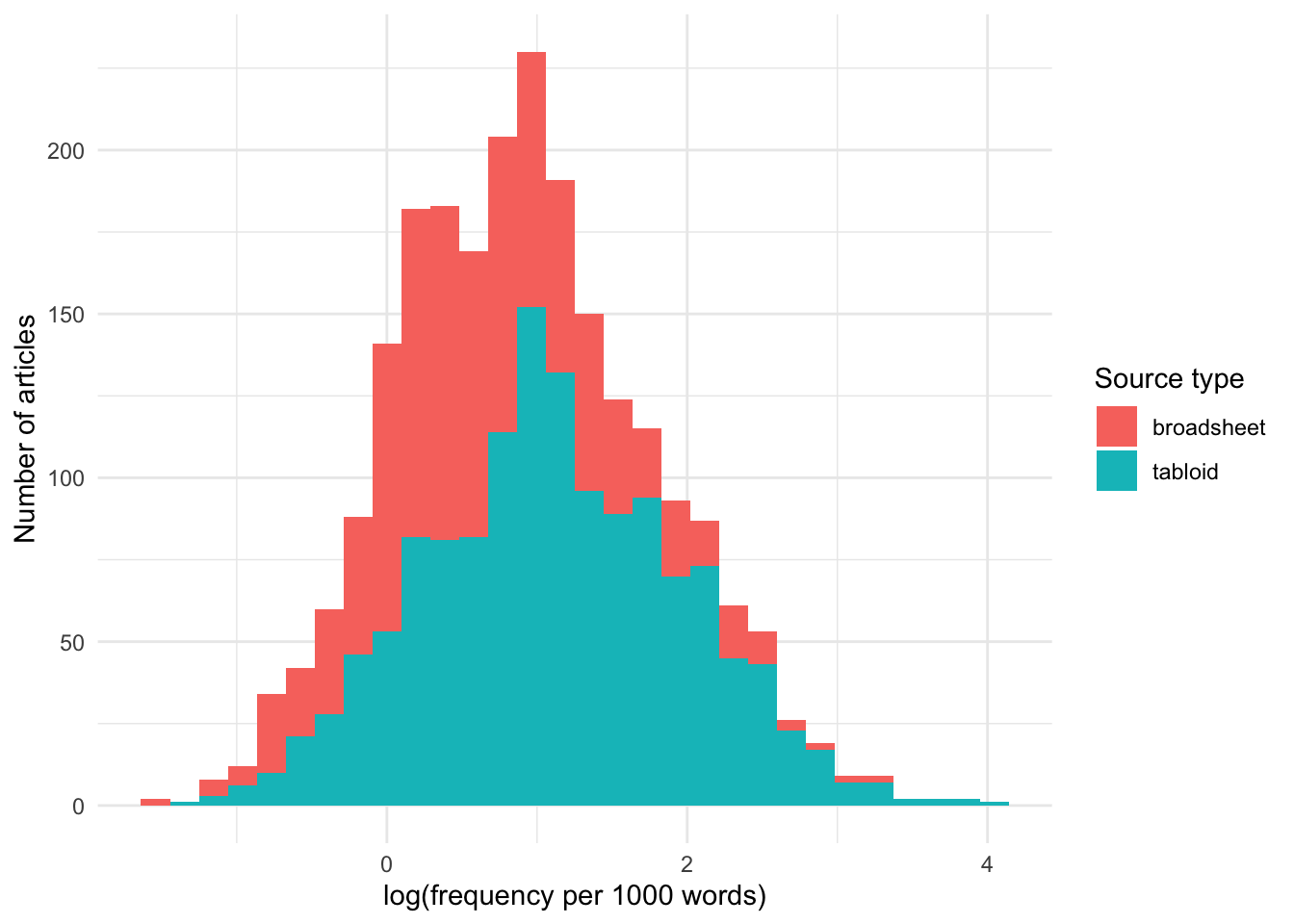
Note that broadsheets have somewhat longer texts than tabloids:

Code

fat_annotated_filtered %>%
  ggplot(aes(x = source_type, y = log(wordcount_total))) + 
  geom_boxplot() + 
  labs(
    x = "Source type",
    y = "log(Python word count)"
  )

Figure 5: Boxplot length of articles in tabloids and broadsheets that use FAT.

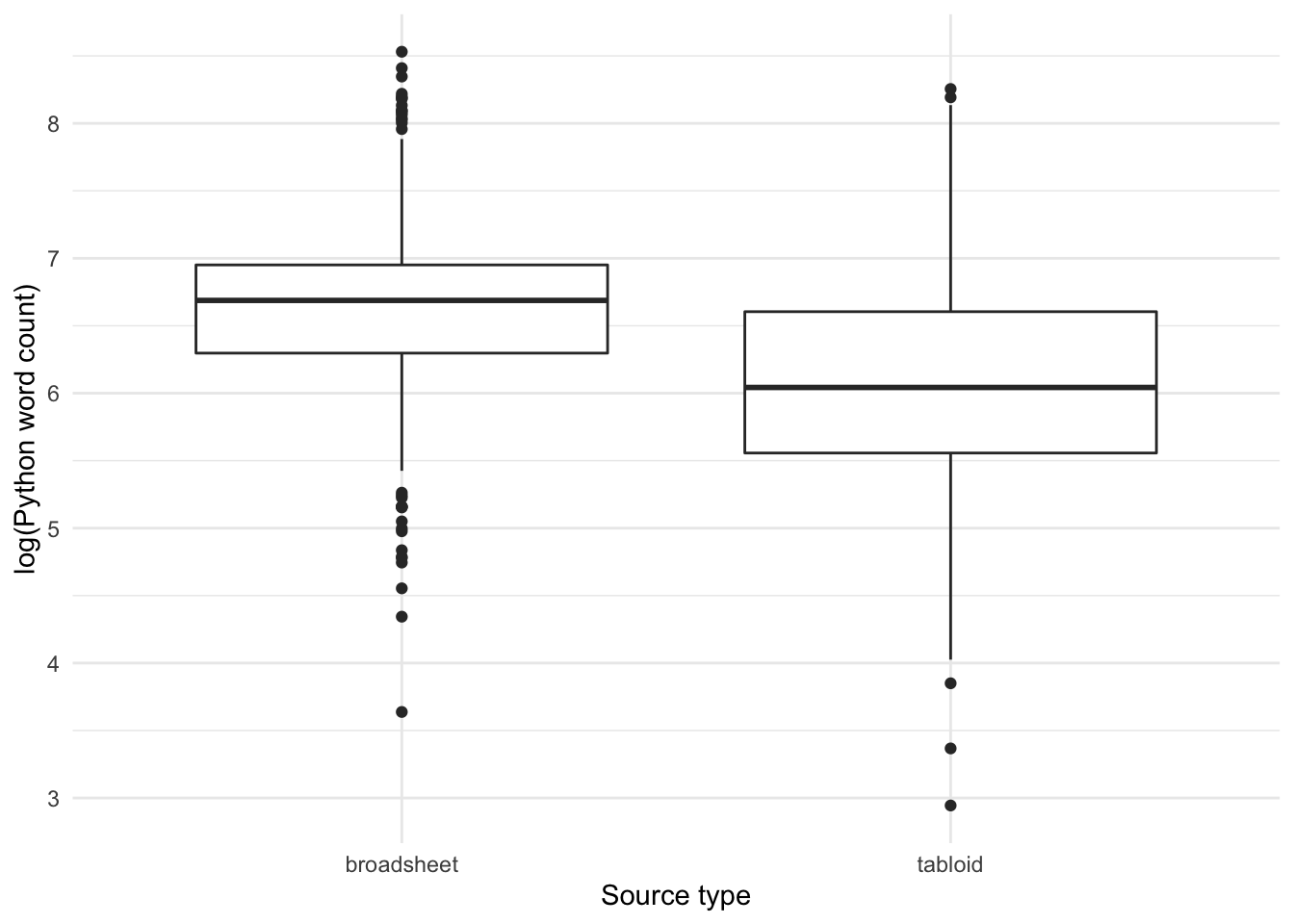
Let’s use a histogram to look at the distribution in more detail:

Code

fat_annotated_filtered %>%
  ggplot(aes(fill = source_type, x = log(wordcount_total))) + 
  geom_histogram(binwidth = 0.1)+ 
  labs(
    y = "Number of articles",
    x = "log(Python word count)"
  )

Figure 6: Histogram of article lengths in tabloids and broadsheets that use the lemma FAT.

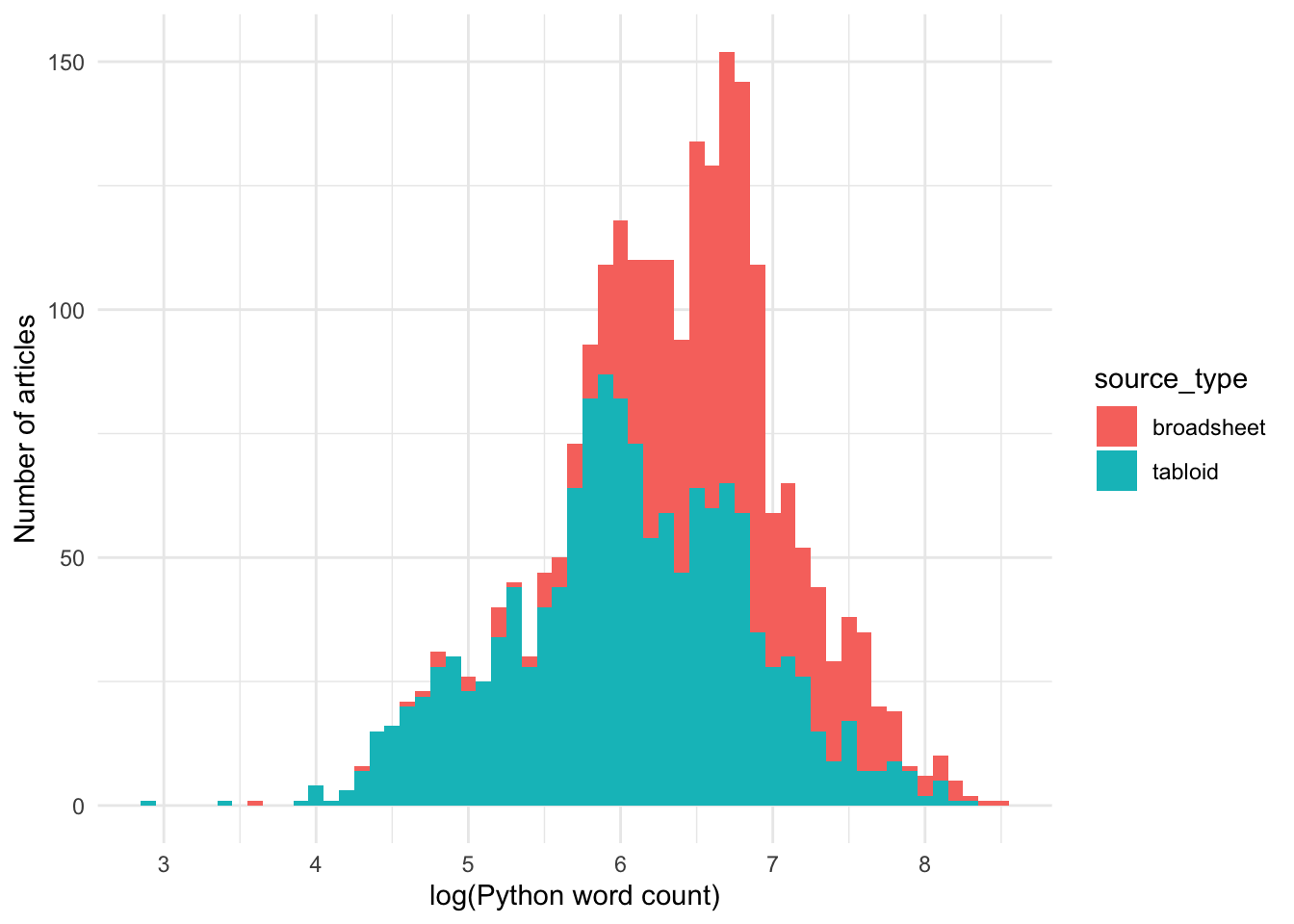
The log-transformed word count data is approximately normally distributed.

Let’s see if the difference in length of articles using the word “fat” in tabloids and broadsheets is significant?

A higher frequency per 1000 words is detected for usage of the word “fat” in tabloids than broadsheets.

Code

frequency_broadsheet <- fat_annotated_filtered[fat_annotated_filtered$source_type == "broadsheet","frequency"] %>% pull()
frequency_tabloid <- fat_annotated_filtered[fat_annotated_filtered$source_type == "tabloid","frequency"] %>% pull()
report::report(t.test(frequency_broadsheet, frequency_tabloid))

The Welch Two Sample t-test testing the difference between frequency_broadsheet and frequency_tabloid (mean of x = 2.62, mean of y = 4.49) suggests that the effect is negative, statistically significant, and small (difference = -1.87, 95% CI [-2.18, -1.56], t(2251.24) = -11.73, p < .001; Cohen’s d = -0.47, 95% CI [-0.55, -0.39])

The non-parametric FP test supports this observation:

Code

fp_test(
  wc1 = frequency_broadsheet,
    wc2 = frequency_tabloid,
    label1 = "broadsheet",
    label2 = "tabloid",
    dist = mydistribution
)


    Approximative Two-Sample Fisher-Pitman Permutation Test
data:  wc by label (broadsheet, tabloid)
Z = -10.336, p-value < 1e-04
alternative hypothesis: true mu is not equal to 0

So, yes, the frequency of use of the word “fat” is lower in broadsheets than in tabloids.

Let’s see if the difference in length of articles using the word “fat” in tabloids and broadsheets is significant?

Code

wordcount_broadsheet <- fat_annotated_filtered[fat_annotated_filtered$source_type == "broadsheet","wordcount_total", drop = T]
wordcount_tabloid <- fat_annotated_filtered[fat_annotated_filtered$source_type == "tabloid","wordcount_total", drop = T]
report::report(t.test(wordcount_broadsheet,wordcount_tabloid))

The Welch Two Sample t-test testing the difference between wordcount_broadsheet and wordcount_tabloid (mean of x = 922.40, mean of y = 573.96) suggests that the effect is positive, statistically significant, and medium (difference = 348.45, 95% CI [301.88, 395.01], t(1740.32) = 14.68, p < .001; Cohen’s d = 0.64, 95% CI [0.55, 0.72])

Yes, overall articles that use the word “fat” in tabloids are significantly shorter than in broadsheets.

The non-parametric FP test supports this observation:

Code

fp_test(
  wc1 = wordcount_broadsheet,
    wc2 = wordcount_tabloid,
    label1 = "broadsheet",
    label2 = "tabloid",
    dist = mydistribution
)


    Approximative Two-Sample Fisher-Pitman Permutation Test
data:  wc by label (broadsheet, tabloid)
Z = 14.462, p-value < 1e-04
alternative hypothesis: true mu is not equal to 0

Let’s use bootstrapping to see if the raw frequencies of usage of the word “fat” are different?

Code

broadsheet_counts <- NULL
tabloid_counts <- NULL
for (i in 1:10000) {
  x <- mean(sample({fat_annotated_filtered %>% 
        filter(source_type == "broadsheet") %>%
      # note sampling 450 here as this is approx 1/2 of broadsheet
        pull(no_hits_in_text)}, 450, replace = FALSE))
  y <- mean(sample({fat_annotated_filtered %>% 
        filter(source_type == "tabloid") %>%
        pull(no_hits_in_text)}, 450, replace = FALSE))
  broadsheet_counts <- c(broadsheet_counts, x)
  tabloid_counts <- c(tabloid_counts, y)
}
counts_comparison <- data.frame(
  mean_sample = c(broadsheet_counts, tabloid_counts),
  source_type = c(
    rep("broadsheet", length(broadsheet_counts)),
    rep("tabloid", length(tabloid_counts))))
counts_comparison %>%
  ggplot(aes(x = mean_sample, fill = source_type)) + 
  geom_histogram()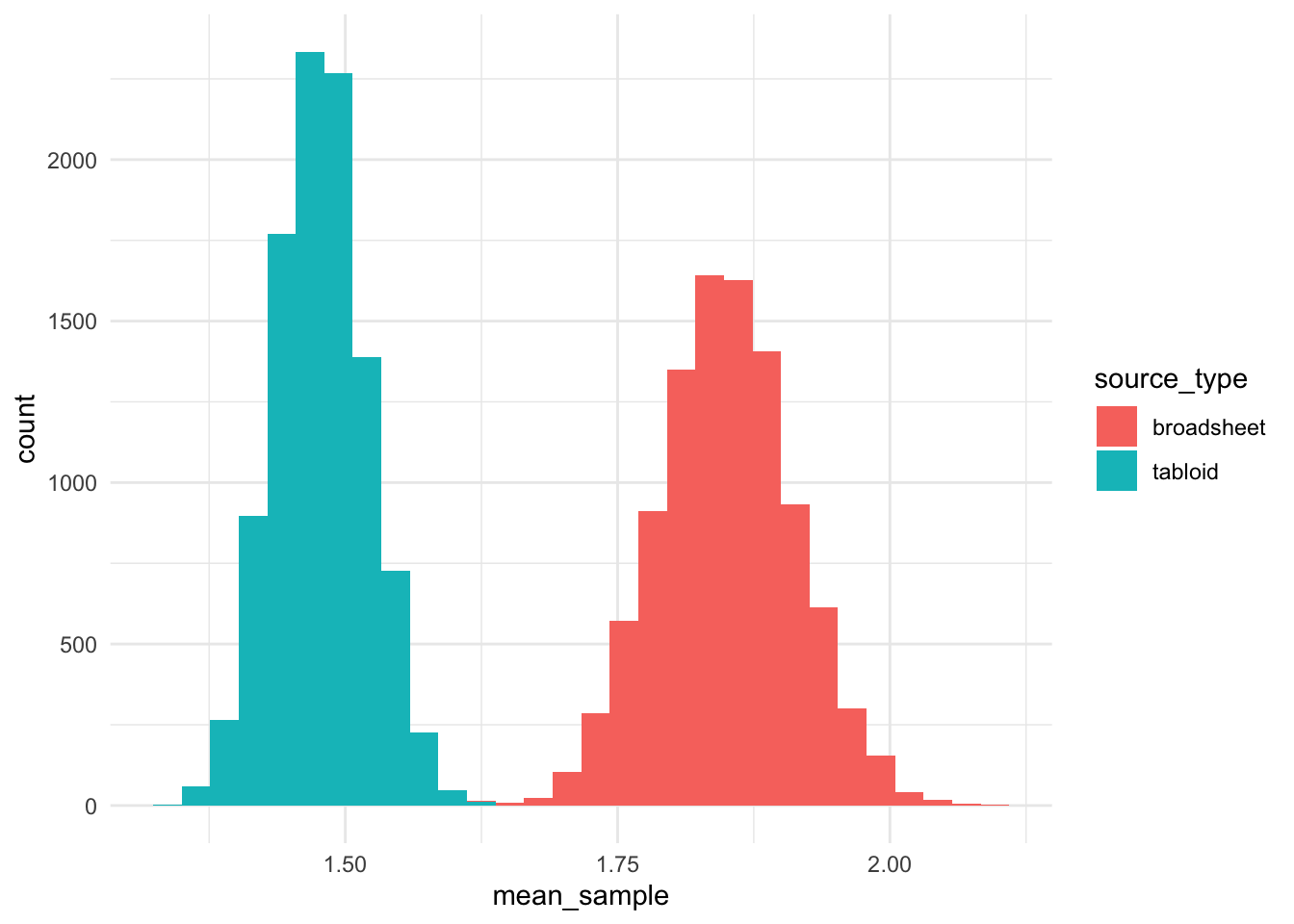

Figure 7: Histogram of sampling of counts per article of the raw frequency of use of FAT in tabloids and broadsheets.

It is interesting how these two distributions do not overlap, and the raw frequencies of the use of the words “fat” in a negative connotation are higher in broadsheets than tabloids. However, the longer length of the articles from broadsheets most likely results in a lower frequency per 1000 words of counts from broadsheets than tabloids.

Code

report::report(
  t.test(
    broadsheet_counts,
    tabloid_counts
  )
)

The Welch Two Sample t-test testing the difference between broadsheet_counts and tabloid_counts (mean of x = 1.85, mean of y = 1.48) suggests that the effect is positive, statistically significant, and large (difference = 0.37, 95% CI [0.37, 0.37], t(17591.34) = 493.31, p < .001; Cohen’s d = 6.98, 95% CI [7.67, 7.67])

The non-parametric FP test supports this observation:

Code

fp_test(
  wc1 = broadsheet_counts,
    wc2 = tabloid_counts,
    label1 = "broadsheet",
    label2 = "tabloid",
    dist = mydistribution
)


    Approximative Two-Sample Fisher-Pitman Permutation Test
data:  wc by label (broadsheet, tabloid)
Z = 135.94, p-value < 1e-04
alternative hypothesis: true mu is not equal to 0

Let’s look at the jittered plot to explore this as well:

Code

fat_annotated_filtered %>%
#| fig-cap: Raw and smoothed frequency of use of FAT in the corpus in tabloids and broadsheets, by year and publication type.
#| label: fig-l10
  ggplot(aes(x = as.factor(year), 
             y = log(frequency), 
             fill = year)) + 
  geom_jitter(alpha = 0.2) +
  geom_smooth(aes(group = source_type), col = "blue", method = "loess") +
  geom_hline(yintercept = 1, col = "red", lty = 3, size = 3) + 
  facet_wrap(~source_type) + 
  theme(axis.text.x = 
          element_text(angle = 90, vjust = 0.5, hjust=1),
        legend.position = "NA") + 
  labs(
    x = "Year",
    y = "log(frequency per 1000 words)"
  )

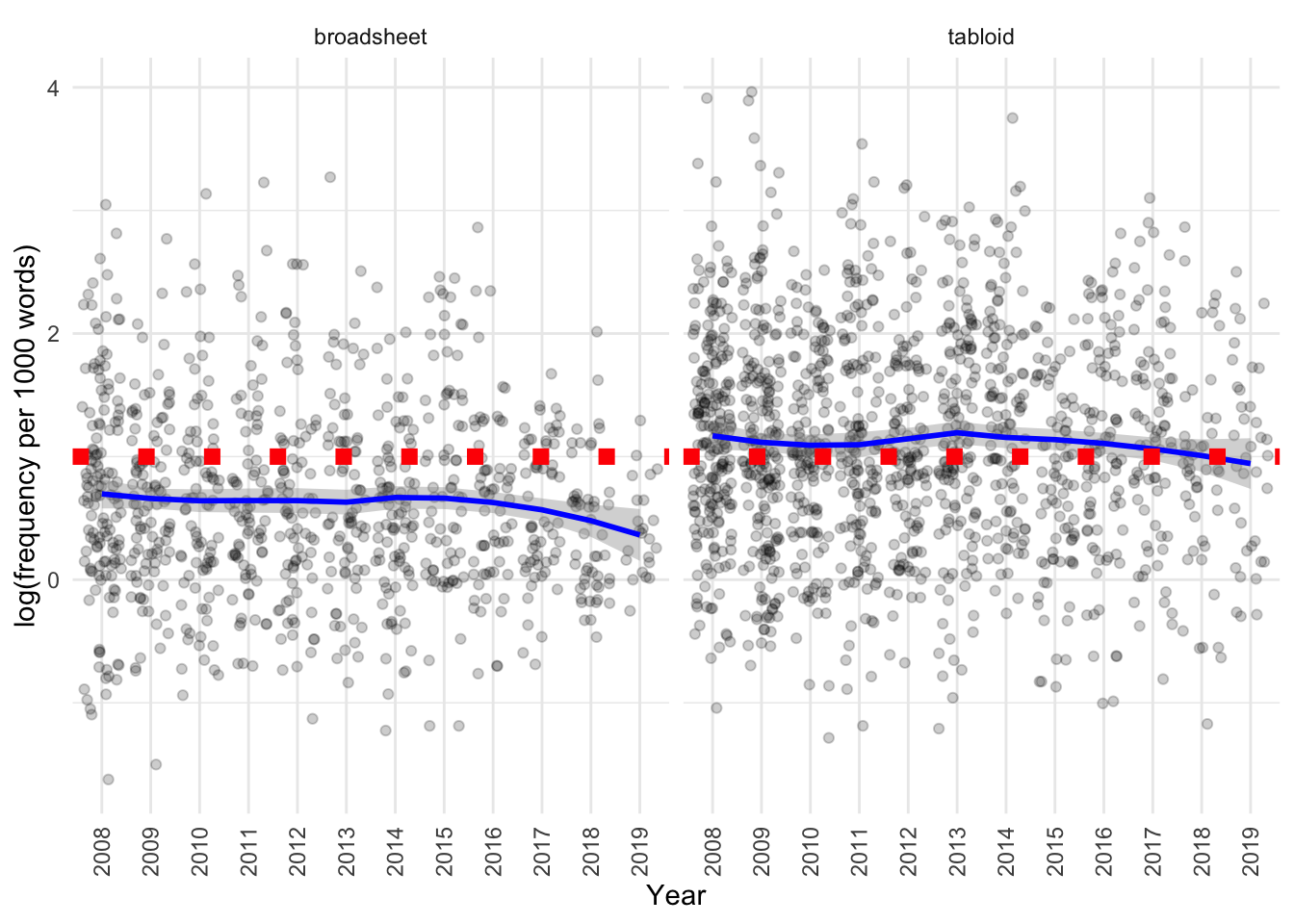
We can see that:

Broadsheets do have a lower frequency per 1000 words than tabloids.
There may be an effect of year for broadsheets but not tabloids with time, with relative frequency decreasing by year.

Comparing observed to normalised to subcorpus size data

We can investigate the prevalence of the use of “fat” using goodness of fit tests, comparing the distribution in:

tabloids vs broadsheets
left and right leaning publications

We can do this by looking at:

the total number of instances in each subcorpus, normalised to the total number of words in each subcorpus
the number of articles that feature this language type, normalised to the total number of articles in each subcorpus

Tabloids vs broadsheets

The total number of uses of “fat” we observe is higher in tabloids and lower in broadsheets than we would expect based on the word count in these subcorpora (p < 0.001).

Code

chisq_instances_wc_normalised(fat_annotated_filtered, metadata_full, source_type)|> kable()

Table 3: Chi-Squared test for number of uses of FAT in tabloids and broadsheets vs what would be expected given word count across all articles in the publication types.
variable	value
method	Chi-squared test for given probabilities
parameter	1
statistic	80.19926
p.value	3.384939e-19
broadsheet_observed	1698
broadsheet_expected	1971.43313891709
tabloid_observed	2042
tabloid_expected	1768.56686108291

The number of articles with use of “fat” we observe is not different between tabloids and broadsheets.

Code

chisq_articles_totalart_normalised(fat_annotated_filtered, metadata_full, source_type)|> kable()

Table 4: Chi-Squared test for number of articles that use FAT in tabloids and broadsheets vs what would be expected given total number of articles in the publication types.
variable	value
method	Chi-squared test for given probabilities
parameter	1
statistic	0.879783
p.value	0.3482611
broadsheet_observed	918
broadsheet_expected	940.113901311012
tabloid_observed	1382
tabloid_expected	1359.88609868899

Left vs right-leaning publications

The total number of uses of “fat” we observe is higher in right and lower in left-leaning publications than we would expect based on the word count in these subcorpora (p < 0.001).

Code

chisq_instances_wc_normalised(fat_annotated_filtered, metadata_full, orientation)|> kable()

Table 5: Chi-Squared test for number of uses of FAT in left and right leaning publications vs what would be expected given word count across all articles in the publication types.
variable	value
method	Chi-squared test for given probabilities
parameter	1
statistic	29.25461
p.value	6.346508e-08
left_observed	1416
left_expected	1579.37808137617
right_observed	2324
right_expected	2160.62191862383

The number of articles that use “fat” we observe is not different between left and right leaning publications.

Code

chisq_articles_totalart_normalised(fat_annotated_filtered, metadata_full, orientation)|> kable()

Table 6: Chi-Squared test for number of articles that use FAT left and right leaning publications vs what would be expected given total number of articles in the publication types.
variable	value
method	Chi-squared test for given probabilities
parameter	1
statistic	0.9299361
p.value	0.3348795
left_observed	746
left_expected	767.809501968429
right_observed	1554
right_expected	1532.19049803157

Differences in usage by source

Is there a difference in the usage of fat by source?

Code

fat_annotated_filtered %>%
  ggplot(aes(x = reorder(source,frequency), 
             y = log(frequency), 
             fill = source_type)) + 
  geom_boxplot() +
  theme(axis.text.x = 
          element_text(angle = 90, vjust = 0.5, hjust=1),
        legend.position = "NA")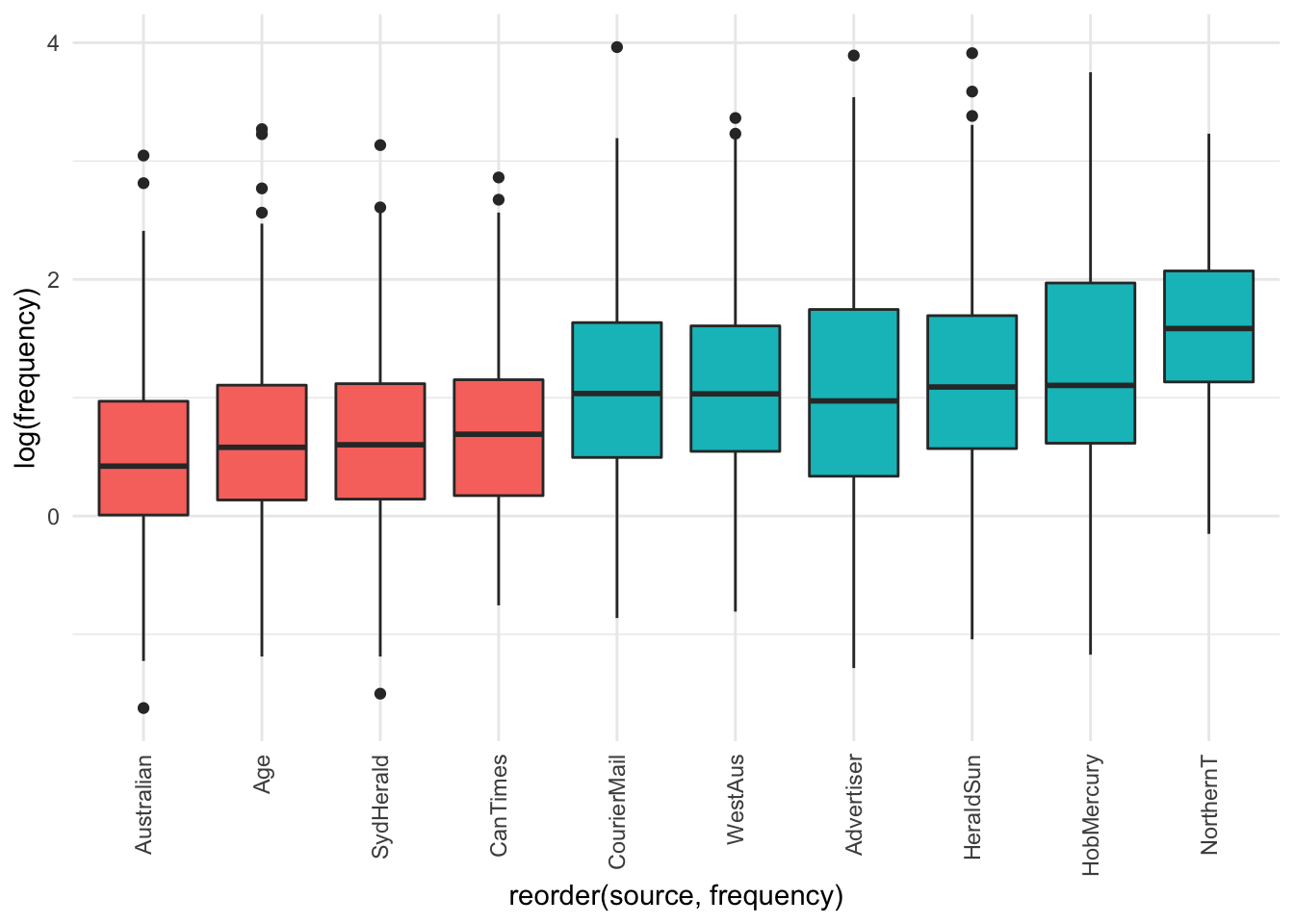

Figure 8: Box plot of usage of FAT by source.

The visualisation suggests there may be some differences, and definitely between tabloids vs broadsheets.

What are the means and standard deviations of the frequency by source?

Code

fat_annotated_filtered %>% 
  group_by(source) %>%
  summarise(
    mean = mean(frequency),
    median = median(frequency),
    sd = sd(frequency),
    type = (source_type)
  ) %>%
  distinct() %>%
  arrange(mean) %>%
  kable()

Table 7: Mean, median and standard deviation of frequency of use of FAT by source.
source	mean	median	sd	type
Australian	2.281607	1.524404	2.481898	broadsheet
Age	2.614527	1.787311	3.036150	broadsheet
SydHerald	2.659197	1.826485	2.634891	broadsheet
CanTimes	2.944274	1.996294	2.861244	broadsheet
CourierMail	4.074611	2.816901	4.354308	tabloid
WestAus	4.155035	2.808989	4.476407	tabloid
Advertiser	4.314423	2.645503	4.884672	tabloid
HeraldSun	4.616753	2.976190	5.133447	tabloid
HobMercury	4.908499	3.017147	5.403502	tabloid
NorthernT	6.287128	4.878049	4.825449	tabloid

It seems that within the different sources among broadsheets there is not much difference among the frequency of use of the word “fat”. Among tabloids, the Northern Territorian seems to have higher frequency of use of “fat” with a negative connotation than other tabloids.

Differences in usage by year

Is there any year when “fat” is used more frequently than others?

Code

fat_annotated_filtered %>%
  ggplot(aes(x = reorder(year,frequency), 
             y = log(frequency), 
             fill = year)) + 
  geom_boxplot() +
  theme(axis.text.x = 
          element_text(angle = 90, vjust = 0.5, hjust=1),
        legend.position = "NA")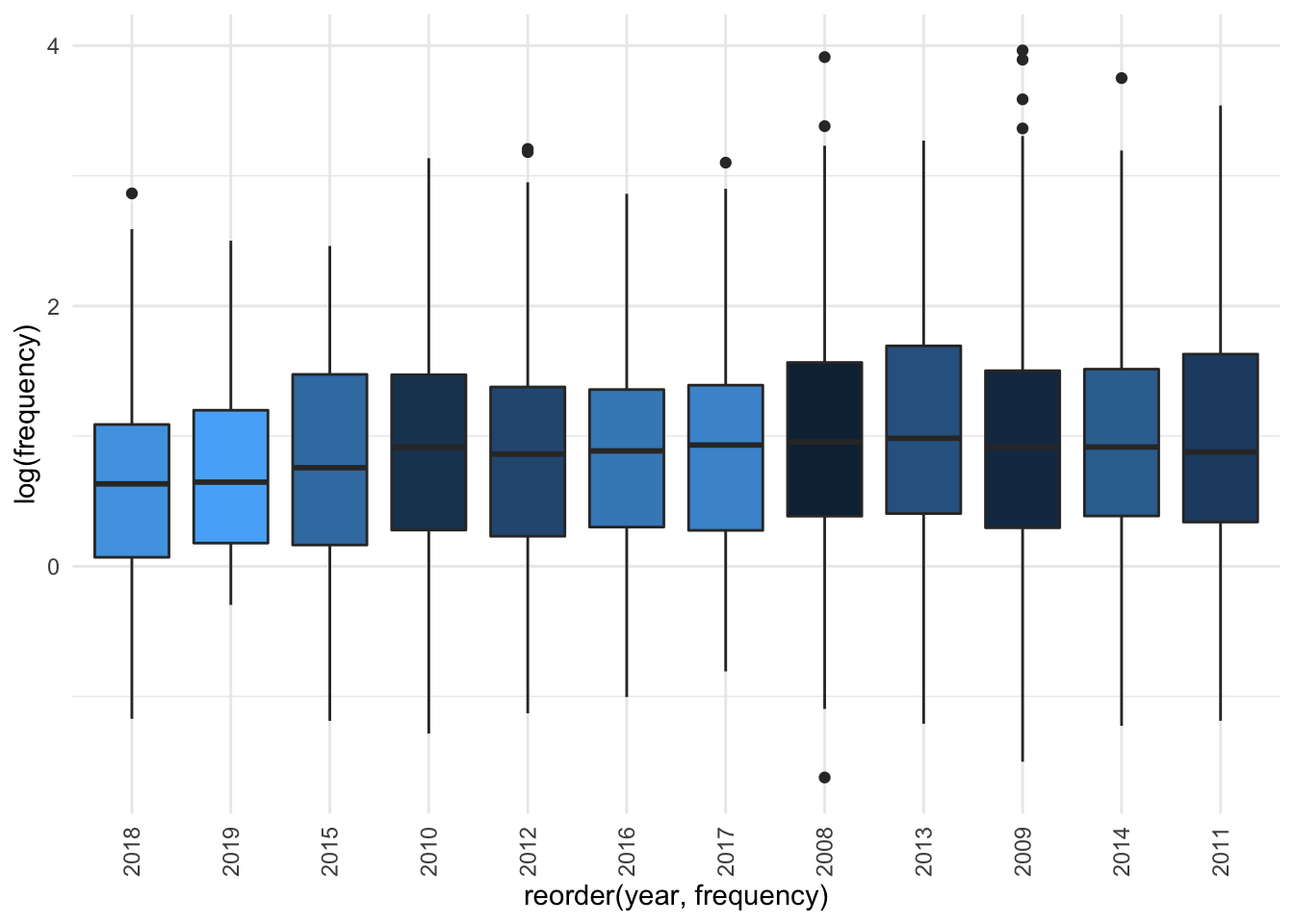

Figure 9: Use of FAT by year, sorted by median use per year from least frequent to most frequent.

Based on the visualisation it seems not. If we separate out by source there also doesn’t seem to be much difference. If we use a jitter plot to visualise the data, then fit a smoothing line and compare with the line of “no change” (dashed red line), we can see that there really isn’t much of a difference by source and year:

Code

fat_annotated_filtered %>%
  ggplot(aes(x = as.factor(year), 
             y = log(frequency), 
             fill = year)) + 
  geom_jitter(alpha = 0.2) +
  geom_smooth(aes(group = source), col = "blue", method = "loess") +
  geom_hline(yintercept = 1, col = "red", lty = 3, size = 3) + 
  facet_wrap(~source) + 
  theme(axis.text.x = 
          element_text(angle = 90, vjust = 0.5, hjust=1),
        legend.position = "NA") + 
  labs(
    x = "Year",
    y = "log(frequency per 1000 words)"
  )

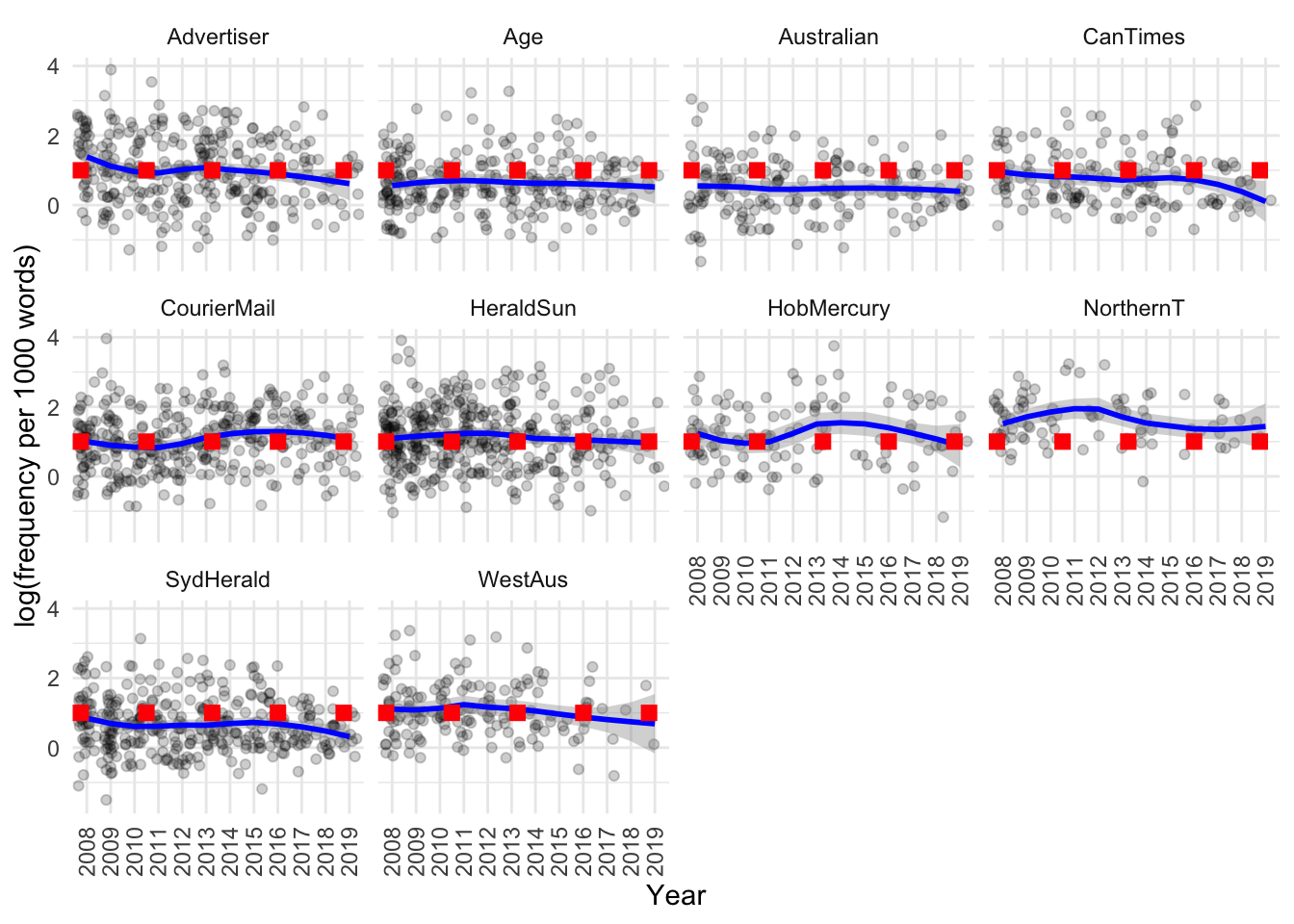
Figure 10: Use of FAT by year and source, split by publication.

There may be a subtle decrease over time in the Advertiser, Age, Canberra Times and Sydney Morning Herald, however, it is unclear whether this trend is very strong.

The distributions each year also look quite similar:

Code

fat_annotated_filtered %>%
  ggplot(aes(x = reorder(year,frequency), 
             y = log(frequency), 
             fill = year)) + 
  geom_violin() +
  theme(axis.text.x = 
          element_text(angle = 90, vjust = 0.5, hjust=1),
        legend.position = "NA")

Figure 11: Violin plot of the distributions of use of FAT by year.

Code

fat_annotated_filtered %>% 
  group_by(year) %>%
  summarise(
    mean = mean(frequency),
    median = median(frequency),
    sd = sd(frequency),
    year = (year)
  ) %>%
  distinct() %>%
  arrange(mean) %>%
  kable()

Table 8: Descriptive statistics of the use of FAT by year across the dataset.
year	mean	median	sd
2018	2.602021	1.883246	2.687849
2019	2.793541	1.908397	2.386139
2015	3.142368	2.132351	2.599177
2010	3.347193	2.493766	3.009772
2012	3.542590	2.366867	3.768130
2016	3.559982	2.425721	3.288919
2017	3.574660	2.538071	3.578586
2008	3.961569	2.597403	4.442870
2013	4.038693	2.673797	4.032539
2009	4.125576	2.496879	5.879841
2014	4.186377	2.500000	5.015075
2011	4.249711	2.403846	4.927228

Differences in usage by source type, source and year

We can also try to simultaneously model differences by source type, source and year.

As expected, a model that includes the source type (tabloid vs broadsheet) gives a better fit than one that does not:

Code

fat_annotated_filtered$scaled_year <- scale(
  fat_annotated_filtered$year, scale = F)
library(lme4)
# base model
m_0_base <- lm(log(frequency) ~ 1, 
                data = fat_annotated_filtered)
# with source type
m_0_sourcetype <- lm(log(frequency) ~ source_type,  
                data = fat_annotated_filtered)
# with year
m_0_year <- lm(log(frequency) ~ scaled_year,  
                data = fat_annotated_filtered)
# with source 
m_0_source <- lm(log(frequency) ~ source,  
                data = fat_annotated_filtered)
# with source and year
m_0_sourceyear <- lm(log(frequency) ~ source + scaled_year,  
                data = fat_annotated_filtered)
# compare
rbind({broom::glance(m_0_base) %>% 
    dplyr::select(-df.residual,- deviance, -nobs) %>%
    mutate(model = "1")},
    {broom::glance(m_0_sourcetype)%>% 
          dplyr::select(-df.residual,- deviance, -nobs) %>%
        mutate(model = "source_type")},
    {broom::glance(m_0_year) %>% 
    dplyr::select(-df.residual,- deviance, -nobs) %>%
    mutate(model = "scaled_year")},
    {broom::glance(m_0_source) %>% 
    dplyr::select(-df.residual,- deviance, -nobs) %>%
    mutate(model = "source")},
    {broom::glance(m_0_sourceyear)%>% 
          dplyr::select(-df.residual,- deviance, -nobs) %>%
        mutate(model = "source_year")}
) %>% 
  dplyr::select(model, everything()) %>%
  arrange(AIC) %>%
  kable()

Table 9: Comparison of model summary statistics for simple linear models that incorporate source, scaled year and/or source type.
model	r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC
source_year	0.0957258	0.0917753	0.8221521	24.231192	0.0000000	10	-2807.637	5639.274	5708.162
source	0.0945436	0.0909850	0.8225097	26.567921	0.0000000	9	-2809.139	5640.279	5703.426
source_type	0.0753951	0.0749928	0.8297134	187.385926	0.0000000	1	-2833.206	5672.412	5689.634
scaled_year	0.0029755	0.0025416	0.8615945	6.858039	0.0088823	1	-2919.926	5845.852	5863.074
1	0.0000000	0.0000000	0.8626915	NA	NA	NA	-2923.353	5850.706	5862.187

We can see that the model incorporating source and scaled year provides the best fit for the data, explaining somewhat more variability than that which includes only source or source type.

Code

anova(m_0_base, m_0_sourceyear)

Analysis of Variance Table
Model 1: log(frequency) ~ 1
Model 2: log(frequency) ~ source + scaled_year
  Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
1   2299 1711.0                                  
2   2289 1547.2 10    163.79 24.231 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Code

source(here::here("400_analysis","model_diagnostics.R"))
df_model_resid <- get_model_resid_df(m_0_sourceyear)
diagnostic_lm_plot(df_model_resid)

Figure 12: Plot of model residuals for the fixed effects model log(frequency) ~ source + scaled_year.

Proportion of data points with:

abs(standardized residuals) > 3.29: 0.13%
abs(standardized residuals) > 2.58: 1.09%
abs(standardized residuals) > 1.96: 5.09%

All of these indicate the model is performing reasonably well on the data.

Let’s summarise the model (note that the intercept corresponds to the “first” source, i.e. the Advertiser):

Code

sjPlot::tab_model(m_0_sourceyear)

Table 10: Coefficients and confidence intervals for the fixed effects model log(frequency) ~ source + scaled_year.
	log(frequency)
Predictors	Estimates	CI	p
(Intercept)	1.02	0.92 – 1.11	<0.001
source [Age]	-0.39	-0.53 – -0.26	<0.001
source [Australian]	-0.52	-0.68 – -0.37	<0.001
source [CanTimes]	-0.25	-0.41 – -0.09	0.002
source [CourierMail]	0.05	-0.08 – 0.17	0.483
source [HeraldSun]	0.12	-0.01 – 0.24	0.066
source [HobMercury]	0.18	-0.00 – 0.35	0.052
source [NorthernT]	0.59	0.40 – 0.79	<0.001
source [SydHerald]	-0.35	-0.48 – -0.23	<0.001
source [WestAus]	0.06	-0.10 – 0.22	0.489
scaled year	-0.01	-0.02 – 0.00	0.084
Observations	2300
R² / R² adjusted	0.096 / 0.092

This model indicates that the Age, Australian, Canberra Times and Sydney Morning Herald (all broadsheets in the dataset) have lower frequency of usage of the word “fat” with a negative connotation than the Advertiser, whereas the Northern Territorian has a higher usage of the language type.

Code

report::report(m_0_sourceyear)

We fitted a linear model (estimated using OLS) to predict frequency with source and scaled_year (formula: log(frequency) ~ source + scaled_year). The model explains a statistically significant and weak proportion of variance (R2 = 0.10, F(10, 2289) = 24.23, p < .001, adj. R2 = 0.09). The model’s intercept, corresponding to source = Advertiser and scaled_year = 0, is at 1.02 (95% CI [0.92, 1.11], t(2289) = 21.55, p < .001). Within this model:

The effect of source [Age] is statistically significant and negative (beta = -0.39, 95% CI [-0.53, -0.26], t(2289) = -5.62, p < .001; Std. beta = -0.18, 95% CI [-0.24, -0.12])
The effect of source [Australian] is statistically significant and negative (beta = -0.52, 95% CI [-0.68, -0.37], t(2289) = -6.66, p < .001; Std. beta = -0.22, 95% CI [-0.29, -0.15])
The effect of source [CanTimes] is statistically significant and negative (beta = -0.25, 95% CI [-0.41, -0.09], t(2289) = -3.07, p = 0.002; Std. beta = -0.13, 95% CI [-0.20, -0.06])
The effect of source [CourierMail] is statistically non-significant and positive (beta = 0.05, 95% CI [-0.08, 0.17], t(2289) = 0.70, p = 0.483; Std. beta = -6.33e-03, 95% CI [-0.06, 0.05])
The effect of source [HeraldSun] is statistically non-significant and positive (beta = 0.12, 95% CI [-7.55e-03, 0.24], t(2289) = 1.84, p = 0.066; Std. beta = 0.03, 95% CI [-0.02, 0.09])
The effect of source [HobMercury] is statistically non-significant and positive (beta = 0.18, 95% CI [-1.69e-03, 0.35], t(2289) = 1.94, p = 0.052; Std. beta = 0.06, 95% CI [-0.02, 0.14])
The effect of source [NorthernT] is statistically significant and positive (beta = 0.59, 95% CI [0.40, 0.79], t(2289) = 5.88, p < .001; Std. beta = 0.23, 95% CI [0.15, 0.32])
The effect of source [SydHerald] is statistically significant and negative (beta = -0.35, 95% CI [-0.48, -0.23], t(2289) = -5.46, p < .001; Std. beta = -0.17, 95% CI [-0.22, -0.11])
The effect of source [WestAus] is statistically non-significant and positive (beta = 0.06, 95% CI [-0.10, 0.22], t(2289) = 0.69, p = 0.489; Std. beta = -8.61e-03, 95% CI [-0.08, 0.06])
The effect of scaled year is statistically non-significant and negative (beta = -9.25e-03, 95% CI [-0.02, 1.24e-03], t(2289) = -1.73, p = 0.084; Std. beta = -0.02, 95% CI [-0.03, -9.21e-04])

Standardized parameters were obtained by fitting the model on a standardized version of the dataset. 95% Confidence Intervals (CIs) and p-values were computed using the Wald approximation.

Next, let’s compare if using a mixed model results in improved fit.

Code

m_1_source <- lmer(log(frequency) ~  1 + (1|source), 
                data = fat_annotated_filtered, REML = T)
m_1_source_type <- lmer(log(frequency) ~  source_type + (1|source), 
                data = fat_annotated_filtered, REML = T)
m_1_source_year_type <- lmer(log(frequency) ~  source_type + scaled_year + (1|source), 
                data = fat_annotated_filtered, REML = T)
m_1_source_year <- lmer(log(frequency) ~  scaled_year + (1|source), 
                data = fat_annotated_filtered, REML = T)
m_1_source_year2 <- lmer(log(frequency) ~  scaled_year + (scaled_year|source), 
                data = fat_annotated_filtered, REML = T)
m_1_source_year_type2 <- lmer(log(frequency) ~  scaled_year + source_type+ (scaled_year|source), 
                data = fat_annotated_filtered, REML = T)
rbind(
    {broom::glance(m_0_source)%>% 
          dplyr::select(AIC, BIC, logLik) %>%
        mutate(model = "1 + source")},
    {broom.mixed::glance(m_1_source_year_type)%>% 
          dplyr::select(AIC, BIC, logLik) %>%
        mutate(model = "source_type + scaled_year + (1/source)")},
    {broom::glance(m_0_sourceyear)%>% 
          dplyr::select(AIC, BIC, logLik) %>%
        mutate(model = "scaled_year + source")},
    {broom.mixed::glance(m_1_source) %>% 
    dplyr::select(AIC, BIC, logLik) %>%
    mutate(model = "1 + (1/source)")
    },
    {broom.mixed::glance(m_1_source_year_type2) %>% 
    dplyr::select(AIC, BIC, logLik) %>%
    mutate(model = "source_type + scaled_year + (1/source)")
    },
    {broom.mixed::glance(m_1_source_year) %>% 
    dplyr::select(AIC, BIC, logLik) %>%
    mutate(model = "scaled_year + (1/source)")},
    {broom.mixed::glance(m_1_source_year2) %>% 
    dplyr::select(AIC, BIC, logLik) %>%
    mutate(model = "scaled_year + (scaled_year/source)")},
    {broom.mixed::glance(m_1_source_type) %>% 
    dplyr::select(AIC, BIC, logLik) %>%
    mutate(model = "source_type + (1/source)")
    }
) %>% arrange(BIC) %>%
  kable()

Table 11: Comparison of model summary statistics for linear mixed effects models that incorporate source, scaled year and/or source type.
AIC	BIC	logLik	model
5663.524	5686.486	-2827.762	source_type + (1/source)
5671.055	5688.277	-2832.527	1 + (1/source)
5671.065	5699.768	-2830.532	source_type + scaled_year + (1/source)
5678.552	5701.515	-2835.276	scaled_year + (1/source)
5640.279	5703.426	-2809.139	1 + source
5639.274	5708.162	-2807.637	scaled_year + source
5668.853	5709.037	-2827.426	source_type + scaled_year + (1/source)
5676.593	5711.037	-2832.296	scaled_year + (scaled_year/source)

The model that includes a random intercept for each of the sources and considers source type as a fixed effect provides the best fit based on the Bayesian Information Criterion. Tabloids have a higher usage of the language type.

Code

sjPlot::tab_model(m_1_source_type)

Table 12: Coefficients and confidence intervals for the mixed effects model log(frequency) ~ source_type + 1/source
	log(frequency)
Predictors	Estimates	CI	p
(Intercept)	0.63	0.47 – 0.80	<0.001
source type [tabloid]	0.54	0.32 – 0.76	<0.001
Random Effects
σ²	0.68
τ₀₀_source	0.03
ICC	0.04
N _source	10
Observations	2300
Marginal R² / Conditional R²	0.090 / 0.124

Let’s summarise this model:

Code

report::report(m_1_source_type)

We fitted a linear mixed model (estimated using REML and nloptwrap optimizer) to predict frequency with source_type (formula: log(frequency) ~ source_type). The model included source as random effect (formula: ~1 | source). The model’s total explanatory power is weak (conditional R2 = 0.12) and the part related to the fixed effects alone (marginal R2) is of 0.09. The model’s intercept, corresponding to source_type = broadsheet, is at 0.63 (95% CI [0.47, 0.80], t(2296) = 7.41, p < .001). Within this model:

The effect of source type [tabloid] is statistically significant and positive (beta = 0.54, 95% CI [0.32, 0.76], t(2296) = 4.84, p < .001; Std. beta = 0.22, 95% CI [0.14, 0.31])

Standardized parameters were obtained by fitting the model on a standardized version of the dataset. 95% Confidence Intervals (CIs) and p-values were computed using

The intercepts for for each of the sources were:

Code

coef(m_1_source_type)$source %>% 
  arrange(`(Intercept)`) %>% 
  kable()

Table 13: Intercepts and coefficients for the model log(frequency) ~ source_type + 1/source.
	(Intercept)	source_typetabloid
Advertiser	0.4894885	0.5374269
Australian	0.5108950	0.5374269
CourierMail	0.5297357	0.5374269
WestAus	0.5567112	0.5374269
HeraldSun	0.6025750	0.5374269
Age	0.6235424	0.5374269
HobMercury	0.6516703	0.5374269
SydHerald	0.6575644	0.5374269
CanTimes	0.7443664	0.5374269
NorthernT	0.9743715	0.5374269

Differences in usage by topic

Code

fat_annotated_filtered %>%
  ggplot(aes(x = as.factor(
    reorder(topic_label,frequency)), 
             y = log(frequency), 
             fill = topic_label)) + 
  geom_boxplot() +
  theme(axis.text.x = 
          element_text(angle = 90, vjust = 0.5, hjust=1),
        legend.position = "NA") +
  labs(x = "Topic label",
       y = "log(frequency per 1000 words)")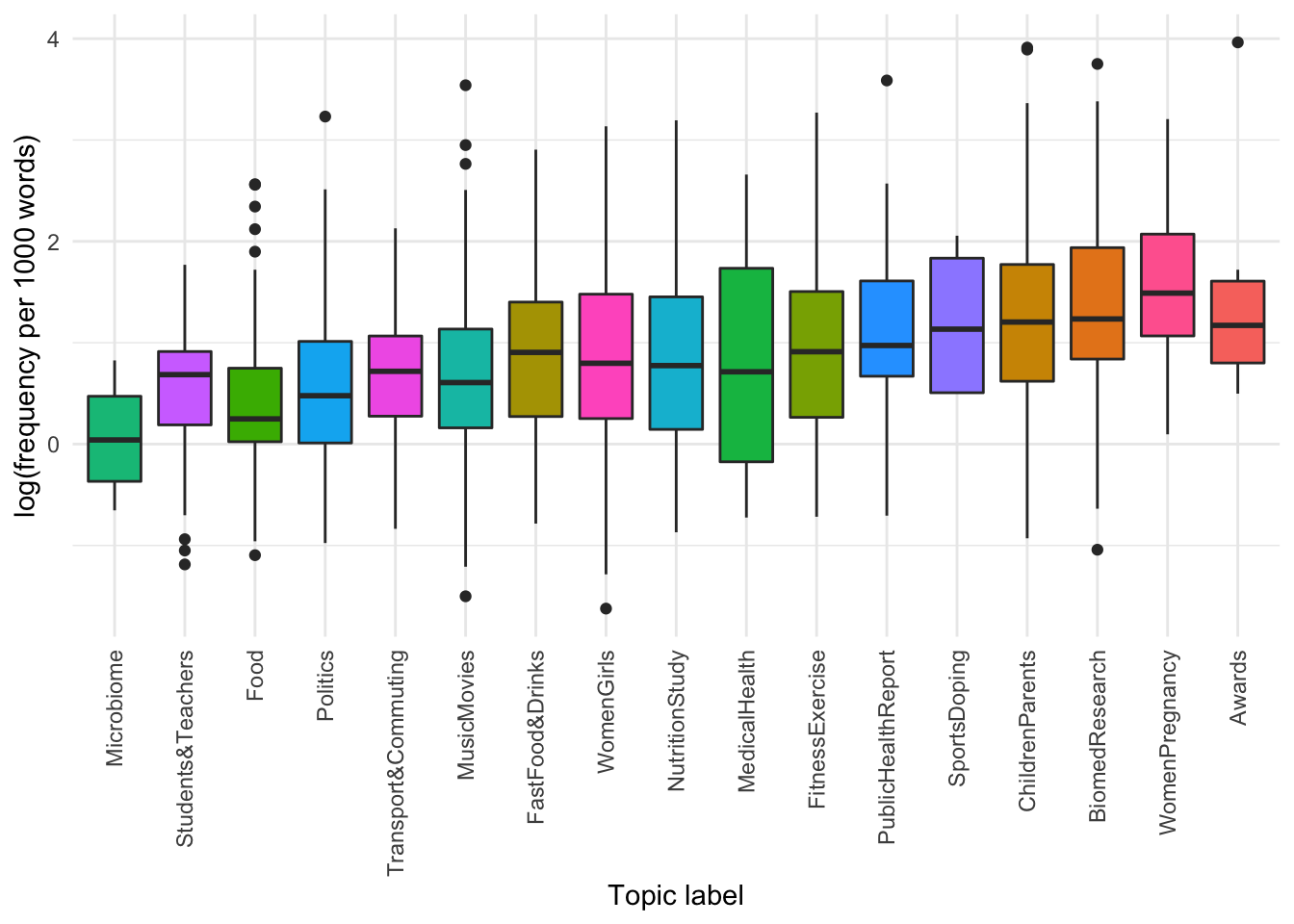

Figure 13: Frequency of use of FAT per 1000 words in articles annotated with specific topic lables.

It seems there are some topics that use fat more than others.

We use a simple linear model with post-hoc comparisons and Bonferroni multiple testing correction:

Code

fat_by_topic <- lm(
  frequency ~ as.factor(topic_label), 
  data = fat_annotated_filtered)
library(emmeans)
fat_by_topic_comp <- emmeans(fat_by_topic, pairwise ~ as.factor(topic_label), adjust = "bonferroni")
fat_by_topic_comp$contrasts %>%
    summary(infer = TRUE) %>%
  filter(p.value < 0.01) %>% 
  kable()

Table 14: Differences in use of FAT in articles annoated with specific topics, with topics compared pairwise with each other.
contrast	estimate	SE	df	lower.CL	upper.CL	t.ratio	p.value
Awards - FastFood&Drinks	7.973995	1.6993808	2283	1.9112363	14.0367536	4.692294	0.0003891
Awards - FitnessExercise	7.631596	1.6893761	2283	1.6045303	13.6586615	4.517405	0.0008948
Awards - Food	9.314549	1.7208689	2283	3.1751289	15.4539691	5.412701	0.0000093
Awards - MusicMovies	8.720687	1.6878559	2283	2.6990449	14.7423289	5.166725	0.0000352
Awards - NutritionStudy	7.918747	1.6962952	2283	1.8669970	13.9704979	4.668260	0.0004371
Awards - Politics	9.122837	1.6967161	2283	3.0695851	15.1760889	5.376761	0.0000114
Awards - PublicHealthReport	7.463489	1.7046693	2283	1.3818625	13.5451149	4.378262	0.0017003
Awards - Students&Teachers	9.378821	1.7908695	2283	2.9896643	15.7679773	5.237021	0.0000242
Awards - Transport&Commuting	9.041890	1.8113633	2283	2.5796197	15.5041610	4.991760	0.0000875
Awards - WomenGirls	7.929696	1.6876047	2283	1.9089498	13.9504419	4.698787	0.0003771
BiomedResearch - FastFood&Drinks	1.892684	0.3814379	2283	0.5318552	3.2535126	4.961971	0.0001019
BiomedResearch - FitnessExercise	1.550285	0.3340530	2283	0.3585078	2.7420618	4.640834	0.0004987
BiomedResearch - Food	3.233238	0.4679631	2283	1.5637195	4.9027563	6.909172	0.0000000
BiomedResearch - MusicMovies	2.639376	0.3262780	2283	1.4753374	3.8034142	8.089348	0.0000000
BiomedResearch - NutritionStudy	1.837436	0.3674470	2283	0.5265222	3.1483505	5.000548	0.0000837
BiomedResearch - Politics	3.041526	0.3693850	2283	1.7236976	4.3593542	8.234027	0.0000000
BiomedResearch - Students&Teachers	3.297510	0.6817724	2283	0.8651994	5.7298200	4.836672	0.0001915
BiomedResearch - Transport&Commuting	2.960579	0.7339189	2283	0.3422297	5.5789289	4.033933	0.0077049
BiomedResearch - WomenGirls	1.848385	0.3249763	2283	0.6889902	3.0077793	5.687753	0.0000020
ChildrenParents - FastFood&Drinks	1.828524	0.4436993	2283	0.2455704	3.4114783	4.121090	0.0053114
ChildrenParents - Food	3.169078	0.5199650	2283	1.3140366	5.0241202	6.094792	0.0000002
ChildrenParents - MusicMovies	2.575216	0.3972800	2283	1.1578688	3.9925638	6.482118	0.0000000
ChildrenParents - NutritionStudy	1.773277	0.4317307	2283	0.2330222	3.3135315	4.107368	0.0056344
ChildrenParents - Politics	2.977366	0.4333814	2283	1.4312228	4.5235099	6.870084	0.0000000
ChildrenParents - Students&Teachers	3.233350	0.7184620	2283	0.6701448	5.7965556	4.500377	0.0009689
ChildrenParents - WomenGirls	1.784225	0.3962117	2283	0.3706892	3.1977613	4.503212	0.0009561
FastFood&Drinks - WomenPregnancy	-2.730627	0.6110072	2283	-4.9104733	-0.5507806	-4.469059	0.0011207
FitnessExercise - WomenPregnancy	-2.388228	0.5826030	2283	-4.4667388	-0.3097170	-4.099237	0.0058345
Food - WomenPregnancy	-4.071181	0.6684492	2283	-6.4559592	-1.6864028	-6.090487	0.0000002
MusicMovies - WomenPregnancy	-3.477319	0.5781800	2283	-5.5400502	-1.4145875	-6.014249	0.0000003
NutritionStudy - WomenPregnancy	-2.675379	0.6023721	2283	-4.8244190	-0.5263398	-4.441407	0.0012734
Politics - WomenPregnancy	-3.879469	0.6035562	2283	-6.0327332	-1.7262048	-6.427684	0.0000000
Students&Teachers - WomenPregnancy	-4.135453	0.8322550	2283	-7.1046292	-1.1662763	-4.968973	0.0000983
Transport&Commuting - WomenPregnancy	-3.798522	0.8754837	2283	-6.9219227	-0.6751220	-4.338770	0.0020335
WomenGirls - WomenPregnancy	-2.686328	0.5774465	2283	-4.7464422	-0.6262135	-4.652081	0.0004725

We can see that there are differences in the frequency of use of the word “fat” by topic, with articles annotated as “Awards”, “Women and Pregnancy” and “Bio-medical Research” using more instances per 1000 words than articles discussing “Students and teachers”, “Politics” and “Food”.